Questo indovinello non ha avuto molto successo… vabbè, speravo ci fosse qualche matematico giocoso in questa orda di blogghettari, ma nulla 🙂
Il testo dell'enigma è qui.
Per scrivere le formule della soluzione ho utilizzato LaTeX. Naturalmente consiglio a tutti di dargli uno sguardo (appena ho un po' di tempo scrivo un tutorial per fare le formule come in questo articolo).
Tanto per cominciare recuperiamo un po' di cosette utili:
Volume della sfera di raggio r: 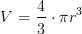
Volume della calotta sferica di raggio r e altezza h: 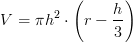
Volume del cilindro di raggio r e altezza h: 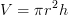
Adesso che abbiamo tutto quello che ci serve, riferendoci al disegno qui sotto, proviamo a calcolare il volume della sfera forata:
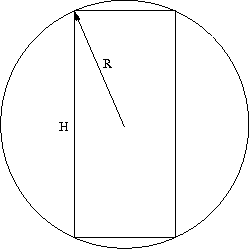
Il rettangolo al centro è il foro che è stato praticato ed è alto H = 6cm come da testo. In più mancano le due calotte sferiche sopra e sotto.
Il problema ci chiede di calcolare il volume totale della sfera meno quello del cilindro e delle due calotte.
Il volume della sfera è: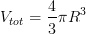
Per calcolare il volume del cilindro ci serve il raggio della sua circonferenza, cioè metà della lunghezza del lato corto del rettangolo. Si può calcolare facilmente applicando il teorema di pitagora fra R e la metà di H: 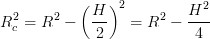
Adesso il volume del cilindro: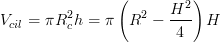
Rimangono le due calotte. Per applicare la formula del volume ci manca l'altezza della calotta. Per ricavarla basta sottrarre al raggio la metà di H: 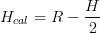
Il volume di una calotta, dopo un po' di passaggi di semplificazione :), sarà:
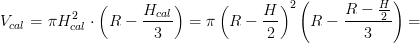
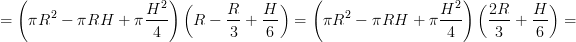
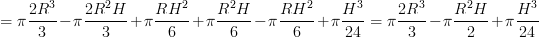
Finalmente possiamo calcolare il volume della sfera forata:
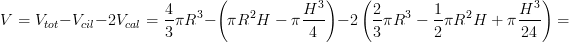
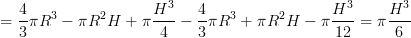
Quindi si semplifica praticamente tutto e il volume finale dipende solo da H. Nel nostro caso H=6cm quindi:
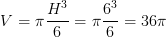
Ma adesso osserviamo il problema da un altro punto di vista: il volume della sfera dipende solo da H (anche il testo del problema ci garantisce questo fatto) ed e' indipendente ad esempio dal diametro del foro. Possiamo allora considerare il caso limite e cioè un foro di diametro piccolissimo (tendente a 0) e altezza H pari al diametro della sfera. In questo caso il volume asportato dalla foratura sarà praticamente nullo e il volume della sfera forata sarà quello di una sfera di diametro H. Ma se il diametro è H allora il raggio sarà la metà di H:
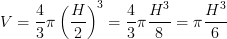
Che è proprio il valore che avevamo ricavato con tanta fatica e tanti calcoli!
A volte basta guardare i problemi da diversi punti di vista… e il mondo ti sorride 🙂

Io la tesi l’ho fatta in TeX e ho continuato ad usarlo per appunti vari scrivendomi le macro per qualsiasi cosa; adesso per scrivere un libro con un mio amico sto cercando di usare ConTeXt e devo ammettere che è una figata… si potrebbe fare un plugin di LifeType per trasformare stringhe $…$ in immagini TeX… ma presuppongo che sia uno sbattone immane… cmq interessante il blog 😉
Le formule sono delle immagini png. Le ho create usando LaTeX, e poi dvipng per convertirle in png. Una volta generate le immagini le ho inserite nelle risorse del blog per poterle pubblicare.
In realtà la mia conoscenza di LaTeX (e TeX) è molto limitata e non va molto oltre l’impaginazione di formuline. Ho scritto la mia tesi di laurea in Context (un’altro macro package tipo LaTeX) di cui chiaramente non mi ricordo quasi nulla… 🙂
A me interessa assai come inserire le formule nelle pagine (sebbene immagino tu abbia usato latex2html…) se ti interessa c’è un plugin per poter scrivere in LaTeX anche in Kopete e in Gaim/Pidgin… spero tu conosca anche il TeX…